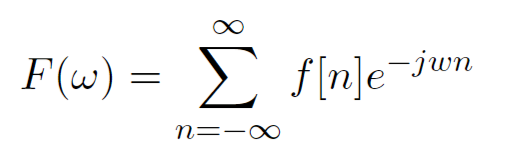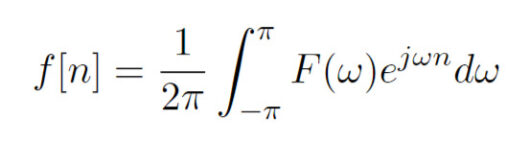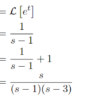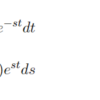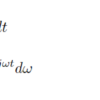ディジタルローパスフィルタの設計をしてみる その7 離散時間フーリエ変換
こんにちは。今回は、離散時間フーリエ変換の内容について勉強していこうと思います。
Contents
離散時間フーリエ変換・逆変換の導入
離散時間信号をf[n]とする。ただしnは整数である。
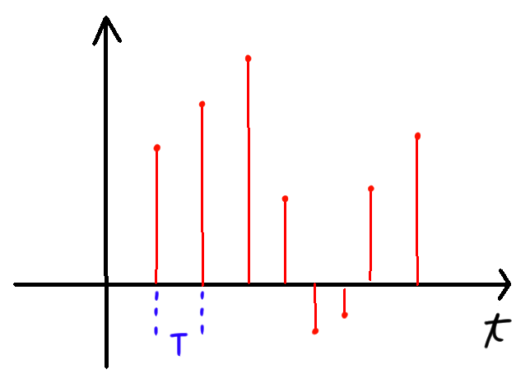
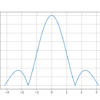
離散時間信号を図で表すと次のように書くことができる。
このとき、区分求積法の考え方を使用してそれぞれの信号を短冊として考えると離散時間フーリエ変換は以下の式で表すことができる。
続いて、離散時間フーリエ逆変換を考える。周期的な時間関数をフーリエ変換すると無限大になりデルタ関数になるため、積分範囲を1周期分にして考えると以下の式を書き下すことができる。
この式を用いてf[n]が計算できることを確認していく。
計算をしていった結果、離散時間フーリエ逆変換ができていることがわかる。
さいごに
久々にブログを更新しました。
書き方を忘れていたこともあり、短めになります。ついに、離散時間の話しに入ることができました。少しずつ、離散時間のローパスフィルタの実装の話しに近づけてきたような気がします。