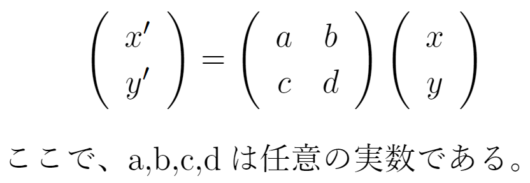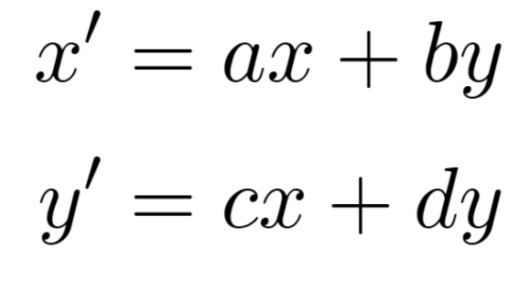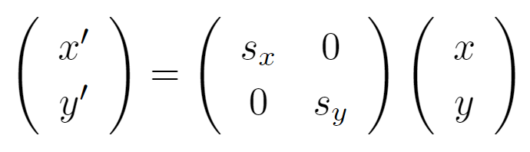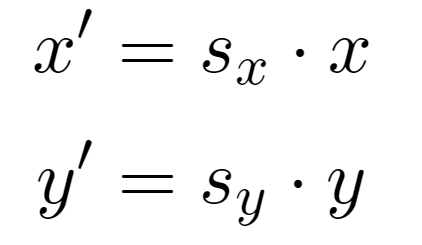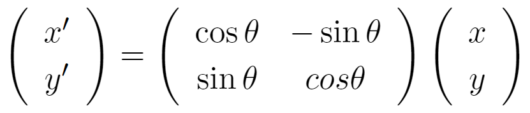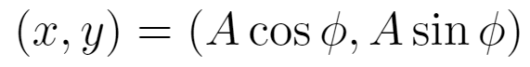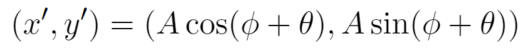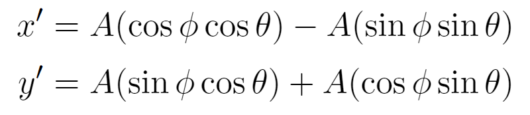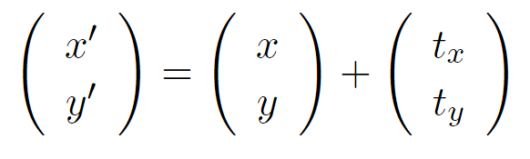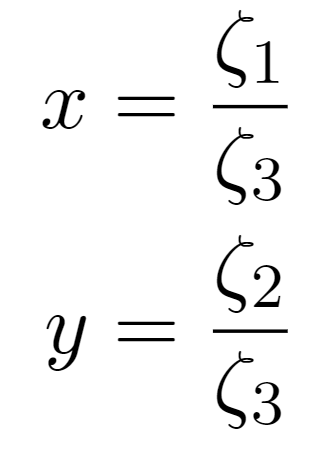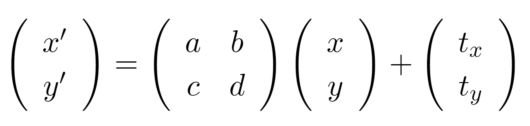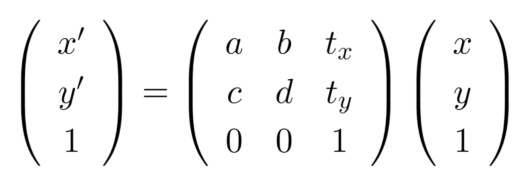画像の幾何学的変換をやってみる その1 回転や拡大などの実装をしてみる
こんにちは。
画像処理の基礎の勉強ということでこれまで平滑化フィルタやエッジ検出フィルタ(微分フィルタ)の勉強、実装をしてきました。今回は、画像の幾何学的変換の実装をしていきたいと思います。線形変換はよくアフィン変換と呼ばれています。包括関係的には射影変換の中にアフィン変換があってその中に線形変換やユークリッド変換があるようです。
今回は、画像の拡大・縮小の実装、回転の実装をします。次回、アフィン変換の実装をしていきたいと思います。
基礎編
線形変換の一般形
座標(x,y)の位置の点が変換により、座標(x’, y’)の位置に移動するとする。そのとき、一般に以下の式で表される変換を線形変換と呼ぶ。
出展:ディジタル画像処理[改訂新版] p158より引用
ディジタル画像処理の内容を引用させていただきました。線形変換を行列で表すと次のようになるのは自明ですね。x’,y’のそれぞれの計算をしてみると次のようになります。
上記の式より、a,dの値を変更すると線形変換した結果はx,yだけに反映され、b,cの値を変更するとy,xについての変換になりそうだということが考えられます。
拡大・縮小について
拡大・縮小は、一般に以下の式で表現される。
出展:ディジタル画像処理[改訂新版] p158より引用
先程の行列を展開した式に代入すると次のようになります。
拡大、縮小ができているということは理解できると思います。先程の、考察は正しそうだということが言えそうです。
回転について
原点を中心に、反時計回りに角度θだけ回転する変換は以下の式で表される。
出展:ディジタル画像処理[改訂新版] p159より引用
この変換用の行列の導出は、三角関数の加法定理と座標をベクトル表現することを考えればわかると思います。行列の掛け算をしてみると次のようになります。
上記の式で回転の移動ができているのかということを考えていきたいと思います。ここで、ベクトルaが以下のように定義されているとします。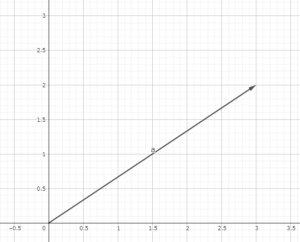
ベクトルaのノルムをA、原点からベクトルまでの角度をφと定義すると、ノルムを使用した座標表示は次のようにできます。
このベクトルaをθだけ回転させると、
ここで、cos(φ+θ),sin(φ+θ)について加法定理を適用して展開すると次のようになります。
この式と、ノルムAの(x,y)座標の表現を見比べてみるとAcosφとAsinφをそれぞれx,yで書き換えることが可能であるということが読み取れます。加法定理を展開した式において適用すると、
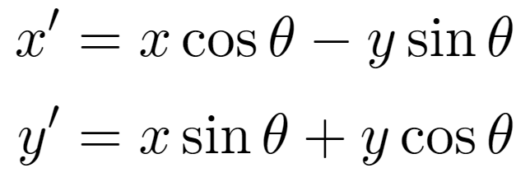線形変換行列を計算して展開したものと同じ形になりました。以上のことから、回転の線形変換はこの行列を使用すれば可能であるといことが理解できました。
平行移動について
画像を平行移動するときの式を以下に示します。
x座標、y座標にそれぞれのオフセット量を足してあげればOKです。
同次座標について
まずは、定義を書いてみようと思います。
座標(x,y)に対し、その要素の数を一つ増やした座標(ζ₁,ζ₂,ζ₃)を、以下の関係式を満たすように定義する。
ただし、ζ₁,ζ₂,ζ₃のうち少なくとも1つは0でないとする。
出展:ディジタル画像処理[改訂新版] p164より引用
アフィン変換の一般形を求めるときに使用するそうです。
アフィン変換について
アフィン変換は、任意の線形変換と平行移動を組み合わせたもののことを言います。同次座標ではなく、線形変換の一般形で表すと次のようになります。
同次座標で表すと次のようになります。
同次座標のときのx’,y’について積を計算してみると線形変換の一般形の計算結果と全く同じ結果になることがわかると思います。
補間について
実装をするにあたって、座標を移動したときに実数になってしまうことがあり得ると思います。しかし、画像の座標はコンピュータの配列を使用する関係上、自然数でアクセスをする必要があります。そのときに、移動後のピクセルの値をどのように決めるのかという点において補間を考える必要が出てきます。
補完の方法には、ニアレストネイバー(最近傍補間)やバイリニア補完(線形補間)があります。ニアレストネイバーでは計算結果に0.5を足して整数を取り出したものを使用する方法1です。バイリニア補完では求めたい位置の周りの4点の画素値を使用して求める方法があります。
今回の実装においては、両方の例を示したいと思います。計算方法等については実装を見た方がわかりやすいと思うためここでは書くことを省略します。
実装してみる
ここまで、基礎編からお付き合いいただいた方はお疲れ様です。初めに、回転と拡大縮小の実装をしていきたいと思います。
環境についてはこちらの記事を見ていただければと思います。
https://garberas.com/archives/1951拡大・縮小
ソースコードを以下に示します。補間にはバイリニア補間を使用しています。
Mat myResize(Mat data, float x_gain, float y_gain)
{
int width = data.size().width;
int height = data.size().height;
int resize_width = (int)((float)width * x_gain);
int resize_height = (int)((float)height * y_gain);
Mat resize_out;
resize_out = Mat::zeros(Size(resize_width, resize_height), CV_8UC3);
for (int x = 0; x < resize_width; x++) {
for (int y = 0; y < resize_height; y++) {
float x_calc = x / x_gain;
int x_check = (int)x_calc;
float dx = x_calc - x_check;
int x_linear = x_calc + 1;
if (x_linear == width) x_linear = width - 1;
float y_calc = y / y_gain;
int y_check = (int)y_calc;
float dy = y_calc - y_check;
int y_linear = y_calc + 1;
if (y_linear == height) y_linear = height - 1;
for (int i = 0; i < 3; i++) {
resize_out.at<Vec3b>(y, x)[i] = data.at<Vec3b>(y_linear, x_linear)[i] * dx * dy;
resize_out.at<Vec3b>(y, x)[i] += data.at<Vec3b>(y_check, x_linear)[i] * dx * (1-dy);
resize_out.at<Vec3b>(y, x)[i] += data.at<Vec3b>(y_linear, x_check)[i] * (1-dx) * dy;
resize_out.at<Vec3b>(y, x)[i] += data.at<Vec3b>(y_check, x_check)[i] * (1-dx) * (1-dy);
}
}
}
return resize_out;
}元画像の横、高さに対して倍率分だけ拡大縮小したすべて0で定義した3色の画像配列を作成して、それぞれの座標ついて求めてバイリニア補完をして画像の拡大縮小を行っています。
回転
ソースコードを以下に示します。補間にはニアレストネイバーを使用しています。
Mat myRotation(Mat data, float deg)
{
int width = data.size().width;
int height = data.size().height;
int rotation_width = 0;
int rotation_height = 0;
if (width > height) {
rotation_width = width;
rotation_height = width;
}
else {
rotation_width = height;
rotation_height = height;
}
float rad = deg * PI / 180.0f;
Mat rotation_out;
rotation_out = Mat::zeros(Size(rotation_width, rotation_height), CV_8UC3);
for (int x = 0; x < rotation_width; x++) {
for (int y = 0; y < rotation_height; y++) {
float x_rota = (x - rotation_width / 2) * cos(rad) -
(y - rotation_height / 2) * sin(rad) + width / 2;
int check_x = (int)roundf(x_rota);
if (check_x > width || check_x < 0) continue;
float y_rota = (x - rotation_width / 2) * sin(rad) +
(y - rotation_height / 2) * cos(rad) + height / 2;
int check_y = (int)roundf(y_rota);
if (check_y > height || check_y < 0) continue;
rotation_out.at<Vec3b>(y, x)[0] = data.at<Vec3b>(check_y, check_x)[0];
rotation_out.at<Vec3b>(y, x)[1] = data.at<Vec3b>(check_y, check_x)[1];
rotation_out.at<Vec3b>(y, x)[2] = data.at<Vec3b>(check_y, check_x)[2];
}
}
return rotation_out;
}先程求めた回転の計算式で計算をしたのち、ニアレストネイバーで座標を決定して置き換えています。関数の入力には直感的に使えるように角度を入力するようにしました。関数内でラジアンに変更しています。また、計算した結果が画像から飛び出している場合は、画素の置き換えをせずに次の処理鬼なるようにしています。
本来であれば必要な幅を計算してから回転処理をすべきかもしれませんね。最初に端の4転移ついて計算して座標をとってあげれば良さそうということが考えられます。
おわりに
アフィン変換を行うにあたって、前処理の計算が少し必要になったため、アフィン変換の実装は次回やっていきます。幾何学的変換は数式をみて、どのような変換が行われるかどうかの雰囲気は簡単に理解できましたが、実際に実装をしようとするとなかなかに難しかったです。アフィン変換の実装を行って今回の記事では紹介をしていない他の線形変換もしてみたいと思います。
参考文献
ディジタル画像処理[改訂新版]