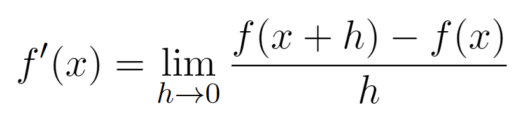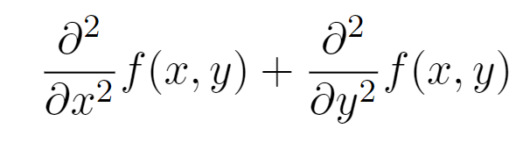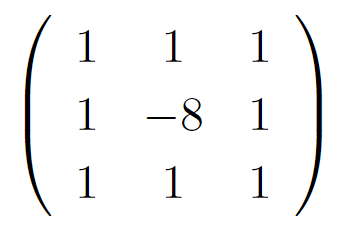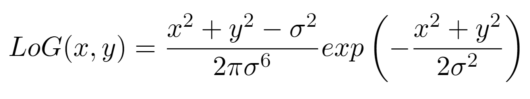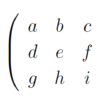画像のエッジ抽出用フィルタを実装してみる その1 空間フィルタリング編
こんにちは。前回は空間フィルタリングの平滑化フィルタの一種であるガウシアンフィルタと平均化フィルタを実装しました。
今回は、空間フィルタリングのエッジ抽出を行うソーベルフィルタとラプラシアンフィルタの実装、LoGフィルタの紹介をしていきたいと思います。
基礎編
エッジ抽出とは
画像中で明るさが急に変化する場所を中抽出することである。これは、画像の特徴や図形を検出したりする前の前処理として利用されるそうです。
具体的に、今回紹介するラプラシアンフィルタをかける前の原画像とラプラシアンフィルタをかけた画像1を以下に示します。
エッジがちゃんと抽出できていることがわかると思います。せっかくなので、OpenCVのラプラシアンフィルタを使用してエッジ検出したものも貼っておきます。
OpenCVのラプラシアンフィルタだと少しぼけて表示されました。自作で作成したものよりもエッジが強く画像に反映されているということ、プログラムを2行書くだけでいいので、OpenCVは便利だなとしみじみ思いました。他に、エッジを綺麗に認識しやすいアルゴリズムであるCannyエッジ検出器を使用してみたときのエッジ検出も確認してみたいと思います。
とてもきれいに検出されていました。おもりのしたのタイヤの反射までもが綺麗に検出されていてびっくりしました。
微分フィルタとは
連続関数における関数f(x)の微分の定義を以下に示す。
関数f(x)が微分可能である場合は、右側、左側微分の極限値が等しくなる。ディジタル画像の場合は、注目画素近傍の差分で置き換えることにより疑似的に微分の処理を行う。したがって、微分フィルタではプラスとマイナスの数値がでてくる。
画像の勾配の向きを設定することで縦方向や横方向に微分フィルタをかけることができる。したがって、フィルタの作り方によって特性が大きく変えることができそうだということが理解できる。
基本的な微分フィルタの例を以下に示す。
ソーベルフィルタについて
先程示した、微分フィルタでは画像の濃淡が急激に変化するエッジの部分を抽出することができるが、画像に含まれるノイズを強調してしまう傾向がある。ノイズを抑えながらエッジを抽出するために、画像の平滑化を平均フィルタを用いて行いながら微分処理を行うフィルタを使用したものをソーベルフィルタと呼ぶ。ソーベルフィルタのフィルタの例を以下に示す。
今回の実装では、上記のフィルタを使用することにした。
ラプラシアンフィルタについて
ラプラシアンフィルタは、二次微分に対応する処理を処理である。通常の演算と同様に微分を2回繰り返す動作を行えばよい。画像の場合は、半画素ずれた画素の差分値を求めるということを行うことが2次微分をしていることと解釈することができるためだ。一般に、関数f(x,y)のラプラシアンは以下の式で定義されている。
これによって、縦、横方向といった方向に依存されないエッジが直接得ることができる。また、実際の実装では8近傍の画素を使用したフィルタを使用されることがあるようなので、今回の実装では以下に示すフィルタ例を使用することにした。
LoGフィルタとは
ラプラシアンは本質的には微分を繰り返すことになるためかなりノイズを強調してしまう。そのため、ガウシアンフィルタを適用してある程度平滑化を行ったのち、ラプラシアンフィルタを施すことが一般によく行われる。
出展:ディジタル画像処理[改訂新版] p111より引用
この2つの処理を一気に計算するものが、LoGフィルタであるそうだ。2次元のガウス分布のラプラシアンの式は、ガウシアンフィルタの式を2階微分することでもとまる。式を以下に示す。
フィルタの実装に関しては、前回のガウシアンフィルタと同様にして行えばよい。
実装を行う
積和演算は、前回の記事と同じ計算なので省略します。今回は、グレースケールとカラーの両方で実行が可能になるようにしてあります。また、今回の微分フィルタでは注目する画素によってはマイナスの値になってしまうことがあります。そのため、マイナスの値になった画素に関しては、値を0にして黒色として表示はしないようにしています。本来は、それぞれの画素の強度等によって色付けて表示をした方がいいと思われますが、今回の実装では考えていないです。
また、前回同様画像の端の処理はしていないため画像の端に関してはエッジ検出が行うことができません。実装によっては端は0埋めにすることもあるようです。
ソーベルフィルタ
フィルタの実装部分を以下に示します。
Mat karnel;
karnel = Mat::zeros(Size(3, 3), CV_32F);
if (direction == 0) {
karnel.at<float>(0, 0) = 1;
karnel.at<float>(0, 2) = -1;
karnel.at<float>(1, 0) = 2;
karnel.at<float>(1, 2) = -2;
karnel.at<float>(2, 0) = 1;
karnel.at<float>(2, 2) = -1;
}
else {
karnel.at<float>(0, 0) = 1;
karnel.at<float>(0, 1) = 2;
karnel.at<float>(0, 2) = 1;
karnel.at<float>(2, 0) = -1;
karnel.at<float>(2, 1) = -2;
karnel.at<float>(2, 2) = -1;
}0埋めの行列を作成して、それぞれの対応する点に値をいれたという感じです。関数の引数によって横、縦方向の設定ができるようになっています。
ラプラシアンフィルタ
Mat karnel;
karnel = Mat::zeros(Size(3, 3), CV_32F);
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
karnel.at<float>(i, j) = 1;
}
}
karnel.at<float>(1,1) = -8;全てを0埋めで行列を作成したのち、すべてに1を設定してから中心のみ値を設定しなおしました。
ソースコード全体
フィルタをかける前に、グレースケールに変換をしてからエッジ検出フィルタをかけています。
Mat convert_gray_scale(Mat img)
{
Mat gray = Mat::zeros(cv::Size(img.cols, img.rows), CV_8UC1);
for (int y = 0; y < img.rows; y++) {
for (int x = 0; x < img.cols; x++) {
// GrayScale = 0.2126R + 0.7152G + 0.0722B
gray.at<uchar>(y, x) = 0.2126f* (float)img.at<Vec3b>(y, x)[2] + 0.7152f* (float)img.at<Vec3b>(y, x)[1] + 0.0722f* (float)img.at<Vec3b>(y, x)[0];
}
}
return gray;
}
Mat mySobelFilter(Mat data, int direction, int color)
{
Mat karnel;
karnel = Mat::zeros(Size(3, 3), CV_32F);
if (direction == 0) {
karnel.at<float>(0, 0) = 1;
karnel.at<float>(0, 2) = -1;
karnel.at<float>(1, 0) = 2;
karnel.at<float>(1, 2) = -2;
karnel.at<float>(2, 0) = 1;
karnel.at<float>(2, 2) = -1;
}
else {
karnel.at<float>(0, 0) = 1;
karnel.at<float>(0, 1) = 2;
karnel.at<float>(0, 2) = 1;
karnel.at<float>(2, 0) = -1;
karnel.at<float>(2, 1) = -2;
karnel.at<float>(2, 2) = -1;
}
#if _DEBUG 1
cout << karnel << endl;
#endif
int height = data.size().height;
int width = data.size().width;
if (color == 1) {
data = convert_gray_scale(data);
}
Mat out = Mat::zeros(Size(width, height), CV_8UC1);
for (int x = 1; x < width - 1; x++) {
for (int y = 1; y < height - 1; y++) {
for (int k = -1; k <= 1; k++) {
for (int l = -1; l <= 1; l++) {
sum_data += (float)data.at<uchar>(y + l, x + k) * karnel.at<float>(l + 1, k + 1);
}
}
if (sum_data < 0.0f) sum_data = 0.0f;
out.at<uchar>(y - 1, x - 1) = (uchar)sum_data;
sum_data = 0.0f;
}
}
return out;
}
Mat myLaplacianFilter(Mat data, int color)
{
Mat karnel;
karnel = Mat::zeros(Size(3, 3), CV_32F);
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
karnel.at<float>(i, j) = 1;
}
}
karnel.at(1, 1) = -8;
#if _DEBUG 1
cout << karnel << endl;
#endif
int height = data.size().height;
int width = data.size().width;
if (color == 1) {
data = convert_gray_scale(data);
}
Mat out = Mat::zeros(Size(width, height), CV_8UC1);
float sum_data = 0.0f;
for (int x = 1; x < width - 1; x++) {
for (int y = 1; y < height - 1; y++) {
for (int k = -1; k <= 1; k++) {
for (int l = -1; l <= 1; l++) {
sum_data += (float)data.at<uchar>(y + l, x + k) * karnel.at<float>(l + 1, k + 1);
}
}
if (sum_data < 0.0f) sum_data = 0.0f;
out.at<uchar>(y - 1, x - 1) = (uchar)sum_data;
sum_data = 0.0f;
}
}
return out;
}おわりに
エッジ検出のフィルタを作成してみました。冒頭にも書きましたがOpenCVを使用する場合は2行程度でできるかつ正しい挙動をしてくれるので、とても助かるなあと思う所存です。ディジタル画像処理の本を読みながら実装をして確認することで理解が深まっているような気がしています。
次は、幾何学的変換の勉強をしていきたいと思っています。
参考文献
ディジタル画像処理[改訂新版]