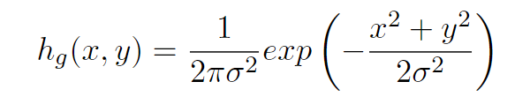画像の平均フィルタとガウシアンフィルタの実装をしてみる
畳み込み演算でカーネルを作成して画像をいじっていきます。OpenCVを使用すれば一行で綺麗に実装が可能ですが、ちゃんとアルゴリズムがどうなっているかどうかを理解したいということで、一つずつそれっぽく実装していきたいと思います。端の処理等はしていないので問題はありますが、今回は基礎的なアルゴリズムを勉強することが目的なので多めに見ていただければと思います。
使用する環境はOpenCV と C++を使用しています。また、OpenCVは画像の読み込みや出力、データ構造を使用しています。
基本概念
空間フィルタリングとは
領域に基づく濃淡変換では、入力画像の対応する画素値だけでなく、その周囲の画素も含めた領域内の画素値を用いて計算する。この処理のことを空間フィルタリング、またそこで用いられるフィルタを空間フィルタとよぶ。
さらに、空間フィルタは、大別すると線形フィルタと非線形フィルタに分けられる。
出展:ディジタル画像処理[改訂新版] p100より引用
ひとつの画素に注目したらその画素の近傍も使用して計算をしていくみたいです。
畳み込み演算とは
フィルタと近傍画素を利用して積和演算を行う計算です。
具体的な計算手順を以下に示します。例では平均フィルタのフィルタを使用しています。
実装をしてみる
早速実装をしていきたいと思います。環境の構築方法はこちらの記事を参考にしていただければと思います。
平均フィルタの実装
平均フィルタの実装したプログラムは以下のようになりました。
/**
* @brief 自作平均フィルタ
* @detail 端の計算処理はしていないため、端の画素は入力画像と同じように表示される。
* 理想は、端の処理をいれることだが、バグフィックスが面倒なためいれていない。
**/
Mat myAverageFilter(Mat data, Size ksize)
{
int height = data.size().height;
int width = data.size().width;
Mat out;
out = data.clone();
uint64_t sumR = 0;
uint64_t sumG = 0;
uint64_t sumB = 0;
for (int x = ksize.width/2; x < width- ksize.width/2; x++) {
for (int y = ksize.height/2; y < height-ksize.height/2; y++) {
for (int k = -ksize.width/2; k <= ksize.width / 2; k++) {
for (int l = -ksize.height/2; l <= ksize.height/2; l++) {
sumB += data.at<Vec3b>(y + l, x + k)[0];
sumG += data.at<Vec3b>(y + l, x + k)[1];
sumR += data.at<Vec3b>(y + l, x + k)[2];
}
}
out.at<Vec3b>(y - ksize.height / 2, x - ksize.width / 2)[0] = sumB / ksize.area();
out.at<Vec3b>(y - ksize.height / 2, x - ksize.width / 2)[1] = sumG / ksize.area();
out.at<Vec3b>(y - ksize.height / 2, x - ksize.width / 2)[2] = sumR / ksize.area();
sumB = 0;
sumG = 0;
sumR = 0;
}
}
return out;
}冒頭に書きましたが、勉強目的のため、端の処理等には目をむけず必ず画素が存在する範囲内でのアクセスを行うようにしています。今回のフィルタは先程の例と同じ平均フィルタのため、フィルタは作成せずに足し合わせたのちにその足し合わせた数で割るという方法で実装をしてみました。愚直にforループの4重ループで実装を行っています。
OpenCVのMat型を使用しています。Mat型についてはcv::Matの基本処理を参考にしていただければと思います。出力用の画像の幅等の設定をするのが面倒だったので画像を深いコピーしたものの画素を変更したものを出力画像としています。
ガウシアンフィルタの実装
画像処理の勉強をすると必ずといっていいほど目にするフィルタです。ガウシアンフィルタは重み付き平均化と呼ばれたりするもので、フィルタの原点に近いほど大きな重みを付けて、遠いほど小さな重みを付けるというフィルタを設計して使用します。
ガウス分布を2次元に拡張した2次元ガウス分布の式を使用してフィルタを作成していきたいと思います。2次元ガウス分布の式を以下に示します。
フィルタのサイズを指定したら、上記の式を使用して自動でフィルタを作成してあげれば良さそうだということがわかりました。実装したプログラムを以下に示します。
/**
* @brief 自作ガウシアンフィルタ
* @detail 端の計算処理はしていないため、端の画素は入力画像と同じように表示される。
* 理想は、端のほうも処理をいれることだが、バグフィックスが面倒なためいれていない。
**/
Mat myGaussianFilter(Mat data, Size ksize, float sigma)
{
Mat karnel;
karnel = Mat::zeros(ksize, CV_32F);
float gause_sum = 0.0f;
// ガウシアンフィルタ用のカーネルを作成
for (int x = -ksize.width/2; x <= ksize.width/2; x++) {
for (int y = -ksize.height/2; y <= ksize.height/2; y++) {
karnel.at<float>(y + ksize.height / 2, x + ksize.width / 2) = (float)exp(-((x * x + y * y) / (2 * sigma * sigma))) / (2 * PI * sigma * sigma);
gause_sum += karnel.at<float>(y + ksize.height / 2, x + ksize.width / 2);
}
}
// スカラー倍をして、和が1になるように落とし込む
karnel = karnel / gause_sum;
#if _DEBUG 1
cout << karnel << endl;
#endif
int height = data.size().height;
int width = data.size().width;
Mat out;
out = data.clone();
float sumR = 0;
float sumG = 0;
float sumB = 0;
for (int x = ksize.width / 2; x < width - ksize.width / 2; x++) {
for (int y = ksize.height / 2; y < height - ksize.height / 2; y++) {
for (int k = -ksize.width / 2; k <= ksize.width / 2; k++) {
for (int l = -ksize.height / 2; l <= ksize.height / 2; l++) {
sumB += (float)data.at<Vec3b>(y + l, x + k)[0] * karnel.at<float>(l + ksize.height / 2, k + ksize.width / 2);
sumG += (float)data.at<Vec3b>(y + l, x + k)[1] * karnel.at<float>(l + ksize.height / 2, k + ksize.width / 2);
sumR += (float)data.at<Vec3b>(y + l, x + k)[2] * karnel.at<float>(l + ksize.height / 2, k + ksize.width / 2);
}
}
out.at<Vec3b>(y - ksize.height / 2, x - ksize.width / 2)[0] = sumB;
out.at<Vec3b>(y - ksize.height / 2, x - ksize.width / 2)[1] = sumG;
out.at<Vec3b>(y - ksize.height / 2, x - ksize.width / 2)[2] = sumR;
sumB = 0.0f;
sumG = 0.0f;
sumR = 0.0f;
}
}
return out;
}先程のプログラムに追加でフィルタの製作を行うプログラムが増えました。フィルタを製作するうえで各係数の総和は1である必要があるので、先程の式で求めたガウス分布のフィルタの総和が1になるようにスカラー倍しています。
さいごに
画像処理を勉強するにあたって使用している本はディジタル画像処理[改訂新版]です。CG-ARTSの画像処理検定の試験用の教本になっており、画像処理の内容が一通りまとまっているようです。過去に、この試験のベーシックは受けて合格したことがあったのでエキスパートに挑戦をしてみようかなと考えています。
また、今回のプログラムの全体をGistに上げたのでリンクをこちらに貼っておきます。
OpenCVがどれだけ偉大かがよくわかりました。自分で実装をする経験等がないとブラックボックスを組み合わせたら完成してしまうので、基礎の勉強には向かない(?)のかなと思いました。この調子で画像処理の基礎的なフィルタ等を実装していきたいと思います。
参考文献
ディジタル画像処理[改訂新版]