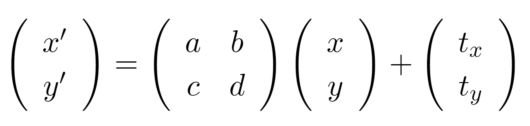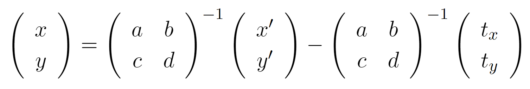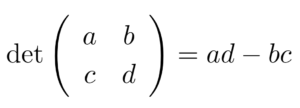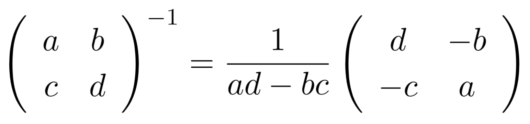画像の幾何学的変換をやってみる　その2　線形変換の一般形を用いたアフィン変換の実装

2020年2月1日2020年7月17日

こんにちは。前回は、幾何学的変換の紹介や拡大・縮小、回転の実装を行いました。

今回は、アフィン変換の実装を行っていきます。アフィン変換の説明も前回の記事で説明しました。内容に関して確認をしたいときは前回の記事を確認していただければと思います。

アフィン変換の実装を行う

実装前の前処理の計算について

アフィン変換の変換行列は以下の式で表されます。

前回の拡大・縮小や回転の実装と同様にこのまま実装を行う場合は、平行移動のことを考えると面倒なことになってしまいます。そのため、ループの中でx,yのときにx’, y’の座標を計算するという手法で実装を行っていけばいいという考えによる実装を行います。式の変形を次のようにします。

これで、求めるためのピースがそろってきました。変換後のx’,y’について考えると回転等の中心は画像の真ん中になることと、逆行列の変換行列の両方から計算して求めることができそうだということがわかる。

逆行列の計算について

ここで、実装を行う前に大切なことがあります。行列において絶対に逆行列が存在するとは限りません。そのため、逆行列が存在するかどうかを判定して実装を行う必要があります。2行2列の行列の行列式を計算すると次のようになる。

また、2行2列の逆行列は次のように求めることができる。

この式より、行列式が0の場合は逆行列が存在しないということがわかる。また、0で割り算を行うことは定義されていないため問題が生じる。これらのことから、アフィン変換の計算を行う前に変換行列に逆行列が存在するかどうかの確認、存在しない場合はエラー処理を行う必要性があるということが理解できる。

コードを書く

ここまでの内容を踏まえて、実装を行うとソースコードは次のようになります。

Mat myAffin(Mat data, Mat conv_matrix, float move_x, float move_y)
{
	double det = determinant(conv_matrix);
	if (det == 0.0f) {
		cout << "逆行列は存在しない。元データを返す" << endl;
		return data;
	}

	Mat inv;

	inv = conv_matrix.inv();

	int width = data.size().width;
	int height = data.size().height;

	Mat affin_out;
	affin_out = Mat::zeros(Size(width, height), CV_8UC3);

	for (int x = 0; x < width; x++) {
		for (int y = 0; y < height; y++) {
			int nowx = x - width / 2;
			int nowy = y - height / 2;

			float rx = (float)nowx * inv.at<float>(0, 0) + (float)nowy * inv.at<float>(0, 1)
				- move_x * inv.at<float>(0, 0) - (float)move_y * inv.at<float>(0, 1) + (float)width / 2;

			int dx = (int)roundf(rx);

			if (dx >= width || dx < 0) continue;

			float ry = (float)nowx * inv.at<float>(1, 0) + (float)nowy * inv.at<float>(1, 1)
				- move_x * inv.at<float>(1, 0) - (float)move_y * inv.at<float>(1, 1) + (float)height / 2;

			int dy = (int)roundf(ry);

			if (dy >= height || dy < 0) continue;

			affin_out.at<Vec3b>(y, x)[0] = data.at<Vec3b>(dy, dx)[0];
			affin_out.at<Vec3b>(y, x)[1] = data.at<Vec3b>(dy, dx)[1];
			affin_out.at<Vec3b>(y, x)[2] = data.at<Vec3b>(dy, dx)[2];
		}
	}
	return affin_out;
}

最初に現在の座標から画像の縦横の幅の半分の値を引いている理由としては、回転等の中心が画像の中心であるためである。また、補間はニアレストネイバーで行っている。変換後のx’,y’の計算は実装処理の前処理の計算についてで出した式を使用しています。

ただし、このアフィン変換の関数ではマシンの幅や高さを変更していないため回転や移動等で範囲外に出た場合は画像が消えるのと同じになってしまいます。これについては、移動後の座標の端を調べてフィットするように画像の高さ、幅をもったものを作成することで問題がなくなると思います。

使用してみる

	Mat data;
	data = imread("画像名");
	if (data.empty()) {
		cout << "Image Data is empty!" << endl;
		return 0;
	}
        Mat conv_matrix;
	conv_matrix = Mat::zeros(Size(2, 2), CV_32F);

	conv_matrix.at<float>(0, 0) = 0.5 * cos(45 * 3.14 / 180);
	conv_matrix.at<float>(0, 1) = 0.5 * -sin(45 * 3.14 / 180);
	conv_matrix.at<float>(1, 0) = 0.5 * sin(45 * 3.14 / 180);
	conv_matrix.at<float>(1, 1) = 0.5 * cos(45 * 3.14 / 180);

	cout << conv_matrix << endl;
	Mat affin_data;
	affin_data = myAffin(data, conv_matrix, 0.0f, 0.0f);
	imshow("affin convertion", affin_data);

この例では回転と縮小の両方を行っています。このように、変換行列や平行移動のパラメータを設定することで様々な変換ができます。

色々な処理を各自で行っていただければと思います。

さいごに

幾何学的変換で有名なアフィン変換の実装が完了しました。プログラミングに落とし込むにあたって、逆行列を計算したりと式変形を頑張る必要があるので、実装に落としこむためにはいろいろなテクニックが必要になるということがわかりました。画像処理は、数式をみて雰囲気の理解はできても実装となると手が出しずらかった理由のひとつがこのテクニックだったのかなと思い始めました。

次は、ヒストグラムや濃度変換または、2値化やマスク処理等もやってみたいと思います。