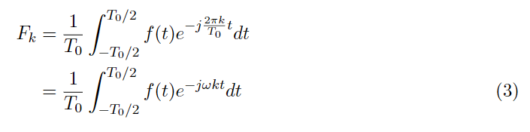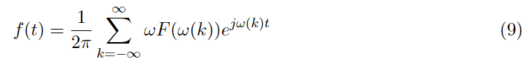ディジタルローパスフィルタの設計をしてみる　その3 フーリエ変換の勉強

2020年12月29日

こんにちは。前回まで2回かけてフーリエ級数展開の勉強をしたので、今回はフーリエ変換の内容に入っていきます。
前回の記事(フーリエ級数展開の話)↓




フーリエ変換とフーリエ逆変換

フーリエ変換・逆変換を式(1),式(2)に示す。
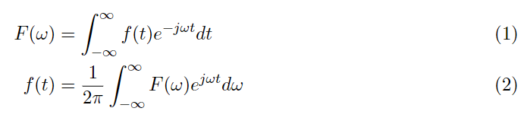フーリエ変換・逆変換の導出をしていく。前回の複素指数関数を用いたフーリエ級数展開のフーリエ係数F_kを求める式を式(3)に示す。

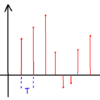
このF_kの絶対値をとったものを振幅スペクトル、偏角をとったものを位相スペクトルといい、矩形波の場合は以下の図のようになった。(n=10のとき　左からの順に振幅スペクトル、位相スペクトル、フーリエ級数展開の計算結果をプロットしたものになる。)
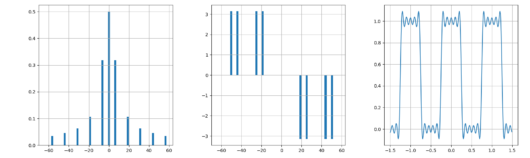続いて、式(4)にフーリエ級数展開の式を再掲する。
式(4)が言っていることは、先ほどのF_kにe^{jωkt}を書けたものを足し合わせるということであり、k=1,2,…のときは振幅スペクトルのように非連続で値が出現していることになり、連続にはならない。ここで、波形を変えずに基本周期T_0を2倍にすると、振幅スペクトルの数は2倍になることが式(5)よりわかる。
同様に、基本周期T_0を無限大までもっていくと周期的な信号とは言えなくなるが、振幅スペクトルは周波数領域で見ると連続なスペクトル形状は連続になるのではないかということが考えられます。
ここで、式(4)に対して区分求積法の考え方を使用して総和を計算する問題から面積を計算する問題に置き換えるということを行います。
式(4)において、区分求積法の考えを用いて式変形をすると、

ここで、式(6)を変形するにあたって式(7),式(8)のように変数を置き換えることを考えます。
式(6)を式(7),式(8)を用いて表すと、

式(9)をωの積分として書き換えると、
フーリエ逆変換の式が導出できました。続いて、式(3)を式(7),式(8)を用いて表すと
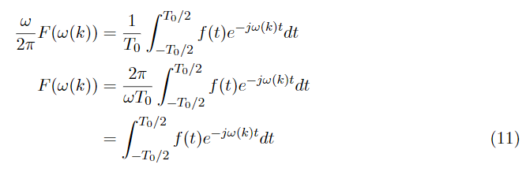このとき、式(11)の積分区間を無限大に飛ばすと、

フーリエ変換の導出ができました。
連続時間の関数f(t)を周波数領域の関数F(ω)に変換することをフーリエ変換、その逆を行うことがフーリエ逆変換になっていることがわかりました。

さいごに

ディジタルフィルタの設計までに、勉強することは山ほどあるので積み重ねていこうと思います。フィルタ設計にたどり着くときの記事のナンバリングがいくつになるのかが今から楽しみだなぁ・・・。
次回は、フーリエ変換の計算やプログラムの実装などをしていく予定です。

参考文献

ディジタル通信　コロナ社