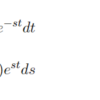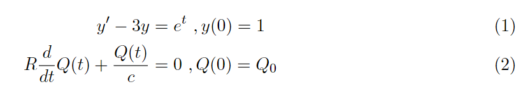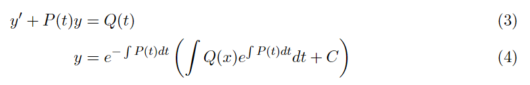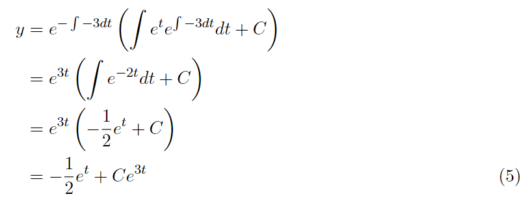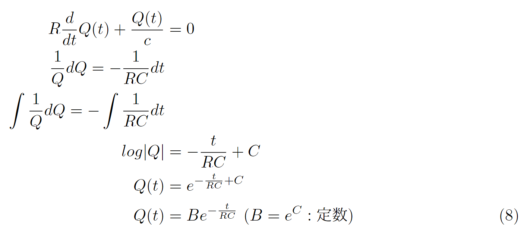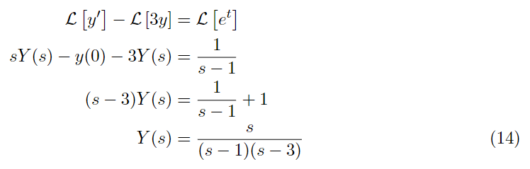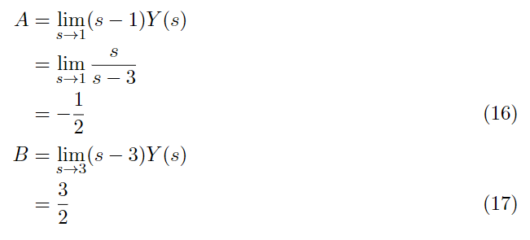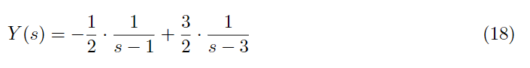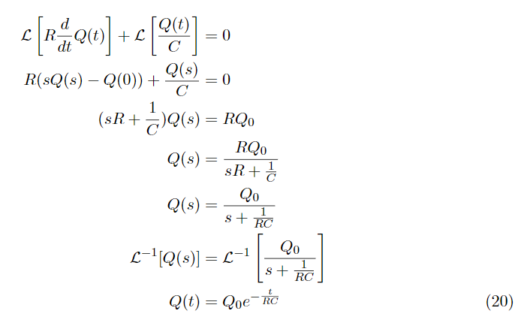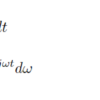ディジタルローパスフィルタの設計をしてみる その6 ラプラス変換を用いて微分方程式を解く
こんにちは。前回はラプラス変換の勉強をしました。
今回はラプラス変換を用いて微分方程式を解くってことをやっていきたいと思います。
Contents
微分方程式を解いてみる
式(1),式(2)を解いていきたいと思います。
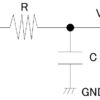
まずは、微分方程式をラプラス変換を用いずに解いてみます。式(2)はコンデンサの放電のときの微分方程式です。
微分方程式の作法に則った解法
式(1)の場合
式(3)の一般解が式(4)で解くことができることを用いて計算をしていきます。
式(5)と初期値を用いて積分定数を求めると、
式(5),式(6)より、式(1)の微分方程式の特殊解は
式(2)の場合
変数分離形の微分方程式として解くことができます。
式(8)に初期値を代入すると、
ラプラス変換を微分方程式に使うための前準備
ラプラス変換、逆変換をそれぞれ式(11),式(12)のように表すことがあります。
ラプラス変換の微分則は式(13)のようになります。
式(13)とラプラス変換表を用いて式(1),式(2)を解いていきます。
ラプラス変換を用いた微分方程式の解法
式(1)の場合
ここで、式(14)を式(15)のように部分分数分解ができると仮定します。
式(16),式(17)の結果を式(15)に代入すると、
式(18)をラプラス変換すると、
微分方程式の特殊解が求まりました。
式(2)の場合
式(1)と同様にして解きます。言葉による説明は省略して式の流れを示します。
特殊解が求まりました。
おわりに
ラプラス変換を用いて微分方程式の特殊解を解法をしらなくても、部分分数分解やラプラス変換とラプラス逆変換の対応がわかっていれば導きさせるということがわかりました。
マウスのセンサの情報の扱い方などや制御にも勉強した内容が使えればいいなぁなんて思ったりしながら、ディジタル信号のフィルタの勉強を推し進めています。
参考文献
リンク
リンク