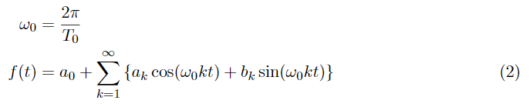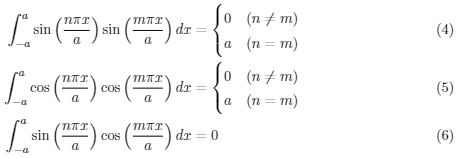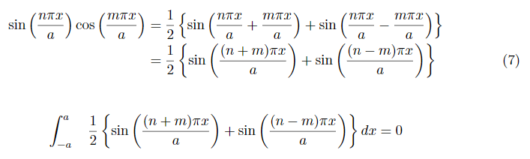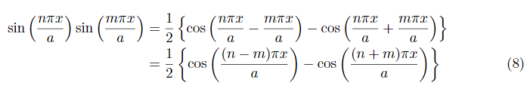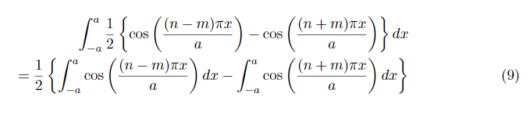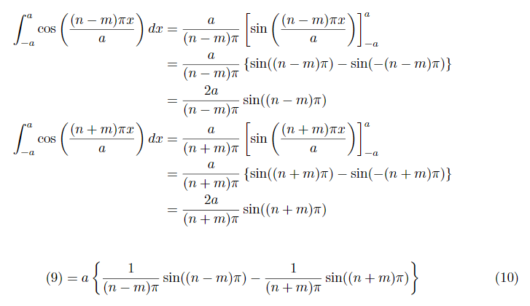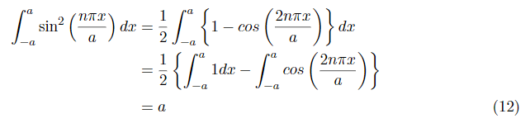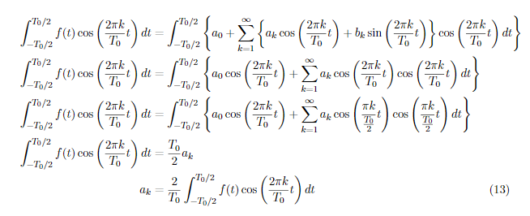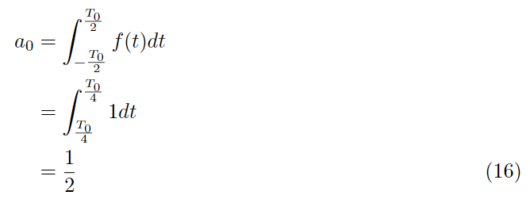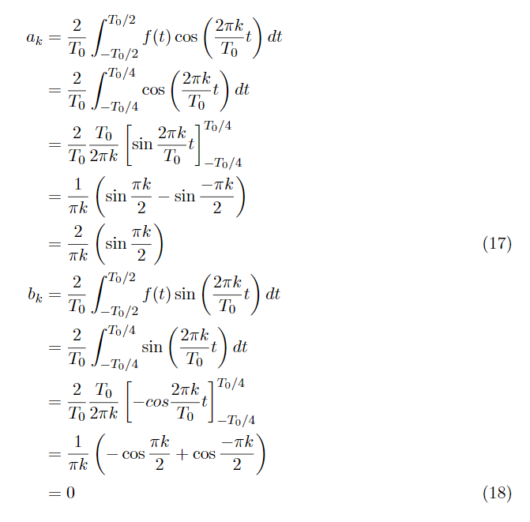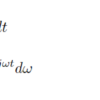ディジタルローパスフィルタの設計をしてみる　その1 フーリエ級数展開の勉強

2020年12月25日2021年7月18日

こんにちは。そらです。
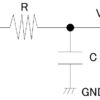
ディジタルローパスフィルタの実装をマイクロマウスでするときに以下のような式で実装をしました。
y[n] = ay[n-1] + (1-a)x[n]
ただし、aは0<a<1、y[n]はフィルタの出力結果、x[n]は現在の入力値です。
最近、とある方からカットオフ周波数はどうなっているの？と聞かれたときに理論的に説明をすることができなかったため原因を探りました。結果としてディジタル信号周りの理解が怪しいことがわかったのでこれを機に勉強をし直すかということで始めました。
今回は、フーリエ級数展開の勉強をしていきたいと思います。プログラムの実装はcやpythonを用いて行います。

間違っている箇所がありましたら、指摘をしていただけるとありがたいです。よろしくお願いいたします。

Contents

1. フーリエ級数展開
2. プログラムの実装をしてみる
3. さいごに
- 3.1. 参考文献

フーリエ級数展開

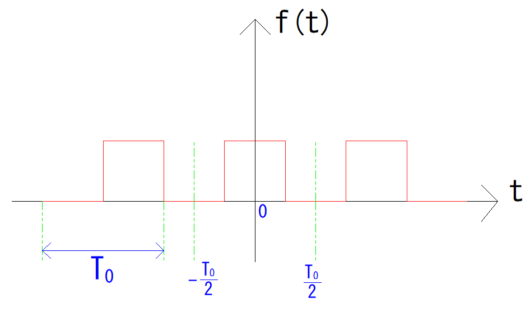
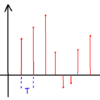
周期的な関数f(t)を考える。今回は例として矩形波を考えます。

フーリエ級数では、周期的な信号がsinとcosの足し合わせで構成されているとすると考えていきます。フーリエ級数展開を式(1)に示します。

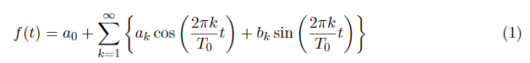角周波数を使ってこの式を変形すると式(2)のようになります。

このことから、kの値が大きくなるにつれてsinとcosの足し合わせに高周波数成分が入ってくるということがわかります。
式(1)、式(2)ででてきたa_0,a_k,b_kのことをフーリエ係数と呼び、それらを求める必要があります。ただし、a_0は一定値ですが、a_k,b_kはkの値によって変わるため適宜計算が必要になることが式よりわかると思います。
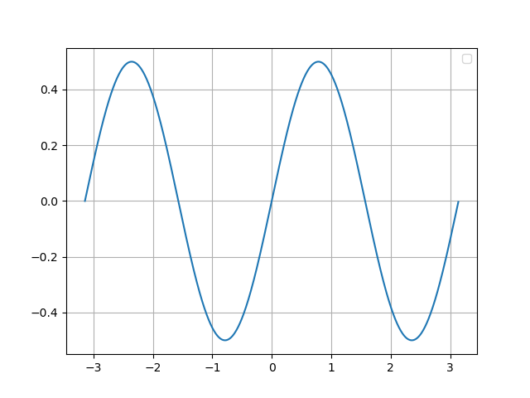
まずは、kの値にかかわらず定数となるa_0の値を求めていきます。積分区間を-T_0/2からT_0/2で(1)式を積分を行います。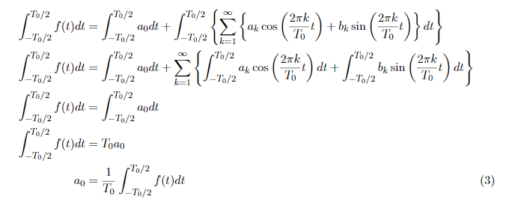式(3)がa_0が求まりました。3回目の式変形でa_kとb_kの含まれる項がすべて消えていますが、任意のkについてsinとcosが-T_0/2からT_0/2の時の積分計算をすると0になります。具体的に数値を入れて積分計算するとそうなりますが、直感的にわかるようにグラフを書いてみます。ここでは、k=1、T_0=1のsin、cosのプロット範囲は-T_0/2からT_0/2グラフを書いてみました。

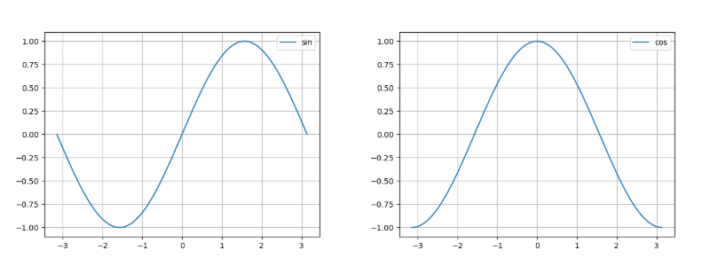
確かに0になることがわかると思います。参考までにグラフを書くのに使用したpythonのプログラムを添付します。

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(-np.pi, np.pi, 0.01)
s = np.sin(x)
c = np.cos(x)

plt.plot(x, s, label="sin")
plt.legend()
plt.grid()
plt.show()

plt.plot(x, c, label="cos")
plt.legend()
plt.grid()
plt.show()

続いてa_kとb_kを求めていきたいと思います。
ここで、式(4)~式(6)の三角関数の関係を使う必要がでてきます。a_kとb_kを求める前に式(4)から式(6)の導出をしていきたいと思います。

式(6)は、sinとcosが直交しているため自明なのですが、式変形及びグラフを書いてみるということをやってみます。
積分の中を式(7)のように積和の公式で式変形をした後、式(6)に代入して積分計算を行うと0になりました。

n = 1, m = 1, a = 3.14の時のグラフをプロットすると以下の図のようになりました。

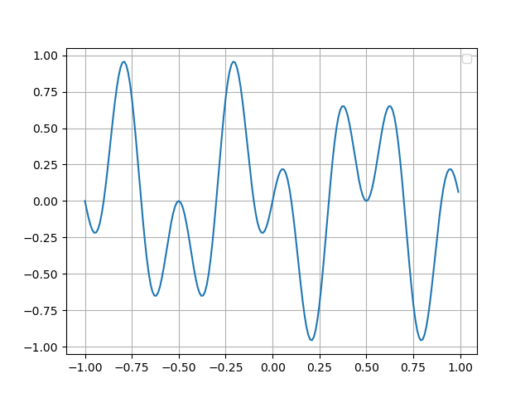
n,m,aの値が違う場合も一つ確認してみたいと思います。n = 2, m = 5, a = 1.0のとき

グラフが0を軸として対象になっていることから積分結果は0になることがわかると思います。

続いて、式(4)の時を式を用いて考えたいと思います。式(5)は余角の公式sin(π/2-θ) = cosθの関係から式(4)が成り立てば式(5)も成り立つことがわかります。
n!=mとn=mのときをそれぞれ考えてみます。

n!=mのとき、(6)同様に積和の公式から式変形をすると式(8)のようになります。

(8)式を(4)式に代入すると、

式(9)の要素ごとに積を行い代入すると

このとき、sin(n-m)π、sin(n+m)πはnとmの値がどのような値であれ0になるため、式(10)は常に0になります。
続いて、n=mのときを考えていきます。n=mのとき(4)式は、

となります。2倍角の公式で式変形をした後、積分を行っていくと、

以上の結果より、式(4)の導出ができた。式(5)も同様に計算すれば同じ結果となる。式(4)~式(6)を再掲する。

フーリエ係数のa_kとb_kを求めていきます。式(1)を再掲します。
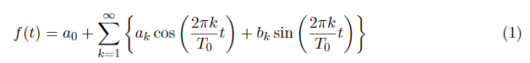ここで、先ほどの式(4)~(6)を用いることでa_kおよびb_kを求めることができます。a_Kを求めたい場合はb_kの項がなくなるように、b_kを求める場合はa_kの項がなくなるようにして、積分を行うということをします。式(13),式(14)にa_K,b_kを求めるために両辺にcos,sinを掛けた式を示します。

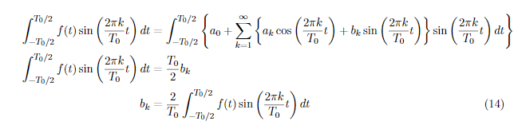以上より、フーリエ級数展開の係数は式(3),式(13),式(14)でできることがわかりました。以下に式を再掲します。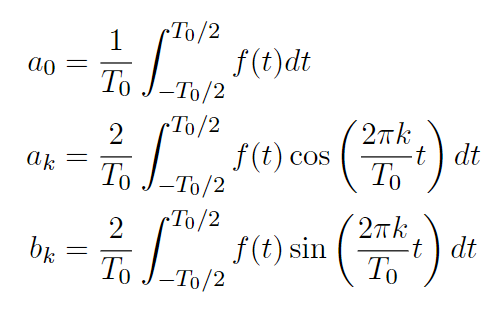

プログラムの実装をしてみる

図を再掲します。

フーリエ係数を求める式とフーリエ級数展開の式を用いて、最初に例として挙げた矩形波のフーリエ級数展開をpythonで実装していきたいと思います。1周期は-T_0/2からT_0/2で考えたいと思います。矩形波の値はf(t)=1とします。場合わけは3通りになります。

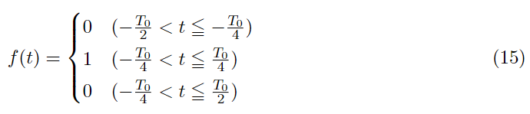
続いてa_0を求めます。場合によって値が違うのでそれぞれの時の計算をします。

続いて、a_kとb_kを求めると

これらを用いて、矩形波の実装を行います。実装したプログラムは以下の通りです。

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(-1.5, 1.5, 0.01)

z = []
y = 0
N = 1000
for i in x:
y = 1/2
for n in range(1,N):
if n % 2 == 1:
y += 2 / (np.pi * n) * np.sin(np.pi * n / 2) * np.cos(2 * np.pi * n * i)

z.append(y)

plt.plot(x, z)
plt.grid()
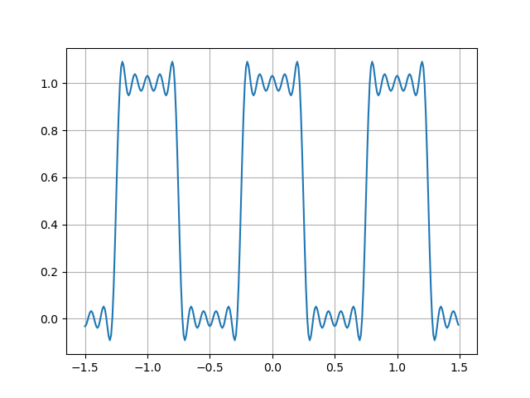
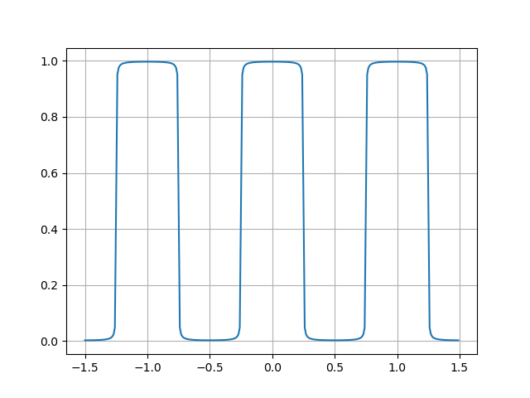
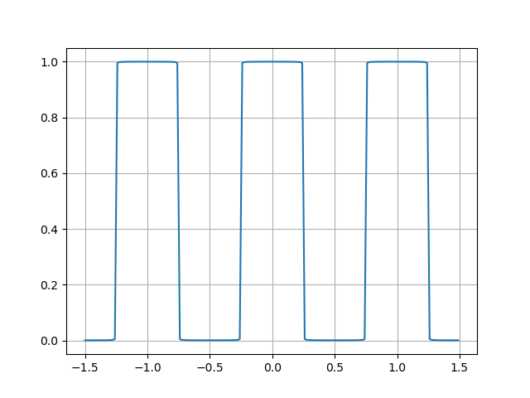
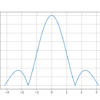
plt.show()

フーリエ級数展開の式のNの大きさによって、f(t)の再現性も変わっていきます。ここでは、N=10,N=100,=1000のときの実行結果を以下に示します。