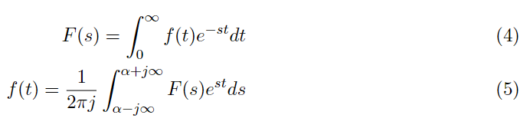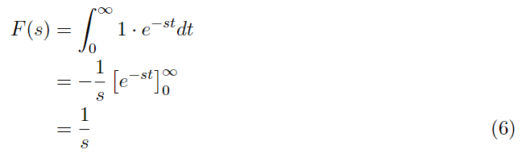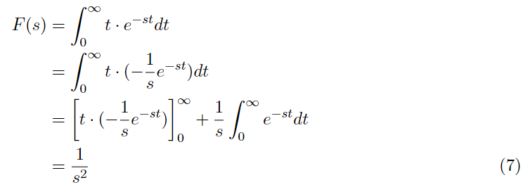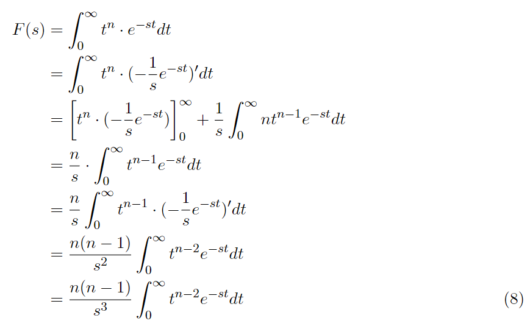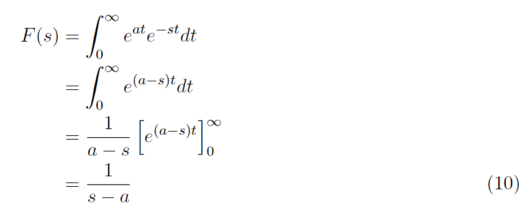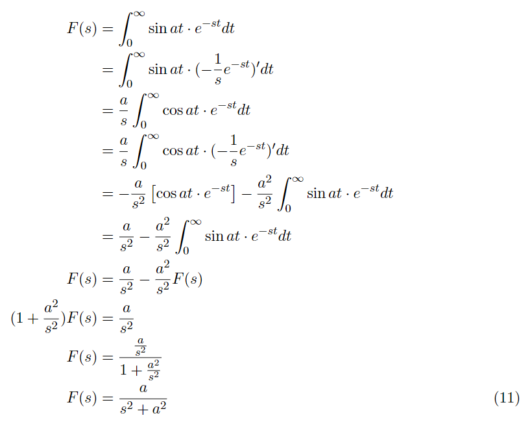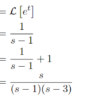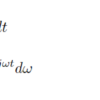ディジタルローパスフィルタの設計をしてみる その5 ラプラス変換の勉強
こんにちは。
今回は、ラプラス変換の勉強をしていきたいと思います。
Contents
ラプラス変換
ラプラス変換の式の導出をフーリエ変換の式から行います。
複素数sのα=0のときにフーリエ変換と一致することがわかり、ラプラス変換がフーリエ変換の拡張であることがなんとなくわかると思います。式(4),式(5)にラプラス変換・逆変換の式を示します。
ラプラス逆変換に関しては、ラプラス変換の結果を用いることが多いため定義式を用いての計算をすることは滅多にないと思います。
ラプラス変換の計算をしてみる
ここからは具体的な関数をラプラス変換していきたいと思います。 大川電子設計製作のホームページのラプラス変換表の表に記載されている関数のラプラス変換をして結果が同じになるか、計算の練習がてらやっていきたいと思います。
f(t)=1
f(t)=t
ｆ(t) = t^n(nは自然数の時)
nに値が代入された場合、n=0になったタイミングで部分積分をしなくてもよい状態、すなわち積分の答えが確定することがわかります。
式(8)までの結果より
となります。この後も同様に積の積分をしていけばわかると思います。
ｆ(t) = e^{at}
f(t) = sin(at)
f(t) = cos(at)の結果は違いますが、sinと同じように積分をしていけばいいだけなのでsinのみ掲載します。
f(t) = e^{bt} sin(at)
f(t) = e^{bt} cos(at)は結果が違いますが、同様に計算することで導出ができるのでsinの場合だけ計算の流れを掲載します。
過去の計算結果が利用のできるところは、積極的に利用していきます。
おわりに
ラプラス変換の導入から計算の練習をしてみました。実際に使用をするときは、ラプラス変換表などを使用するため、ラプラス変換の計算をすることは稀だと思います。
次回は、ラプラス変換を使用して微分方程式を解いてみたいと思います。
参考文献
リンク