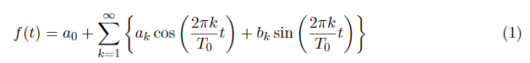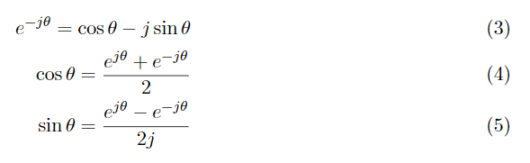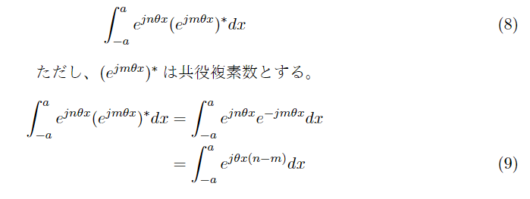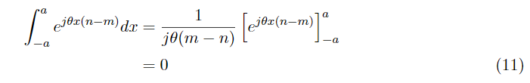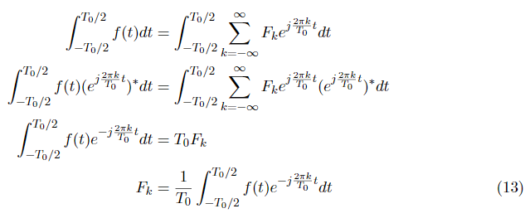ディジタルローパスフィルタの設計をしてみる その2 フーリエ級数展開の勉強の続き
こんにちは。
前回はフーリエ級数展開の勉強をしたのでフーリエ変換に入りたいところですが、その前にフーリエ級数を前回紹介した式とは違う方法で表すということをしていきます。フーリエ変換を導入する前に必要となるためです。
前回の記事↓
複素数を用いたフーリエ級数の導入
初めに、前回のフーリエ級数展開の定義式を再掲します。
続いて、オイラーの公式を紹介します。複素数はjとして、
式(2)では自然対数と複素数と指数関数を用いて複素平面の単位円上の座標を定義することができていることがわかります。sinとcosを式(2),式(3)を用いて複素指数関数で表すと、
式(4),式(5)のようになります。式(1)に代入すると、
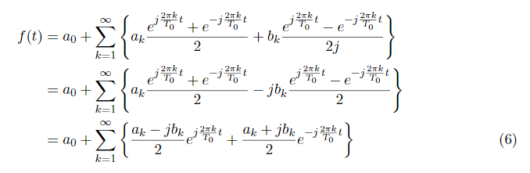 ここで、a_0はk=0のe^{2πkt/T_0}の項であり、式(6)のe^{-j2πkt/T_0}の項は-1から-∞の計算であることと同義であることがわかるので、それぞれの項にかかっているa_kやb_kをまとめてしまうと、
ここで、a_0はk=0のe^{2πkt/T_0}の項であり、式(6)のe^{-j2πkt/T_0}の項は-1から-∞の計算であることと同義であることがわかるので、それぞれの項にかかっているa_kやb_kをまとめてしまうと、
と表すことができる。フーリエ係数を求めるにあたって式(8)を使うことを考える。
n=mのときとn!=mのときをそれぞれ考える。
n=mのとき式(9)は、
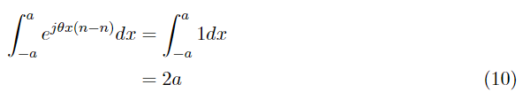 となる。m!=nのとき、
となる。m!=nのとき、
となる。式(10),式(11)より、
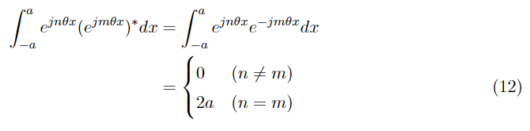 式(12)を用いて式(7)からフーリエ係数F_kを求めることを考えると、
式(12)を用いて式(7)からフーリエ係数F_kを求めることを考えると、
式(13)でフーリエ係数を求めることができるということがわかりました。
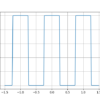
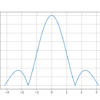
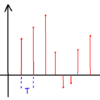
信号を勉強するとよく(周波数)スペクトルという言葉を聞きますが、これは周波数成分に分けられた成分のことを指すそうです。複素指数関数で表すことで、絶対値を考えると振幅スペクトル、偏角を考えると位相スペクトルがでてくるそうです。折角なのでf(t)だけでなく、振幅・位相スペクトルもプログラムで図に表示するということをやってみたいと思います。使用する周期的な関数は前回同様に矩形波を使用することにします。図を再掲します。
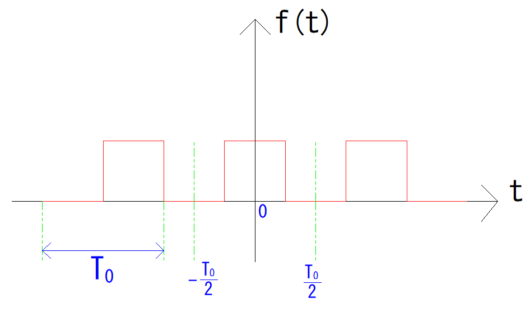 場合わけは式(14)の通り。
場合わけは式(14)の通り。
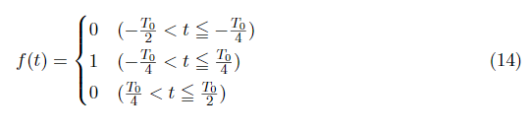 F_kを求めていきます。
F_kを求めていきます。
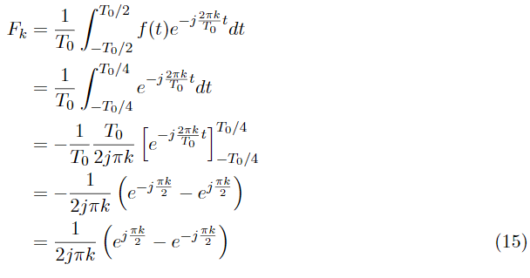
式(15)のようになりました。先ほど求めたF_kでは0のときに0除算が起きてしまうことから、別途F_0を計算する必要があります。F_0(a_0)を計算すると、
プログラムを実装をしていきます。
import numpy as np
import matplotlib.pyplot as plt
import math
import cmath
x = np.arange(-1.5, 1.5, 0.01)
z = []
y = 0
N = 10
T0 = 1
fn = 0
fk = []
fx = np.arange(-N, N, 1)
omega = []
for n in range(-N,N):
if n != 0:
fn = 1/(2 * 1j * np.pi * n) * (np.exp(1j * np.pi * n/2) - np.exp(-np.pi * 1j * n/2))
fk.append(fn)
else:
fk.append(1/2)
omega.append(2 * np.pi * n / T0)
afk = []
pfk = []
for n in range(len(fk)):
if(n%2 == N-1):
afk.append(abs(fk[n]))
pfk.append(0.0)
else:
afk.append(abs(fk[n]))
pfk.append(cmath.phase(fk[n]))
fig = plt.figure()
ax1 = fig.add_subplot(1, 3, 1)
ax2 = fig.add_subplot(1, 3, 2)
ax3 = fig.add_subplot(1, 3, 3)
ax1.bar(omega, afk, width=2.0)
ax1.grid()
ax2.bar(omega, pfk, width=2.0)
ax2.grid()
for i in x:
y = 1/2 + 0j
for n in range(-N,N):
if n != 0:
fn = 1/(2 * 1j * np.pi * n) * (np.exp(1j * np.pi * n/2) - np.exp(-np.pi * 1j * n/2))
y+= fn * np.exp(1j * 2 * np.pi * n * i)
z.append(y)
ax3.plot(x, z)
ax3.grid()
fig.tight_layout()
plt.show()Nの値やT0の値を変えることで重ね合わせや周波数の変更ができます。
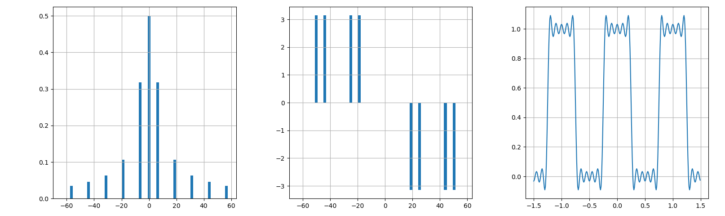
N=10のときの実行結果
 N=1000のときの実行結果(スペクトルは何も見えないので省略)
N=1000のときの実行結果(スペクトルは何も見えないので省略)
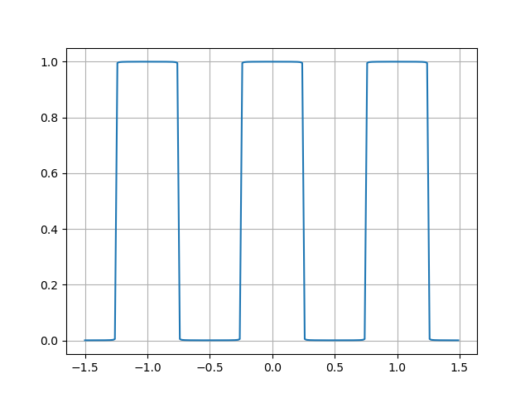 無事矩形波が表示されました。
無事矩形波が表示されました。
おわりに
次回はフーリエ変換の勉強をしていく予定です。数式だらけだー。数式をBlog上で表示しようとしたらエラーが出たので今後も画像を張り付けていきます。
参考文献
ディジタル通信 コロナ社