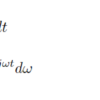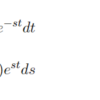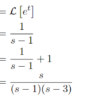ディジタルローパスフィルタの設計をしてみる その4 フーリエ変換の勉強続き
こんにちは。フーリエ変換の勉強の続きをやっていきたいと思います。
前回の記事(フーリエ変換)↓
フーリエ変換を行って、スペクトルをプロットしてみる
前回の記事で、フーリエ変換・逆変換の導出を行いました。今回は、フーリエ変換を行い、スペクトルのプロットをしていきます。フーリエ変換の式を再掲します。
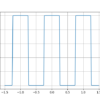
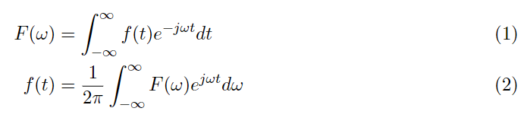 この式を用いて以下の図の信号をフーリエ変換してみたいと思います。
この式を用いて以下の図の信号をフーリエ変換してみたいと思います。
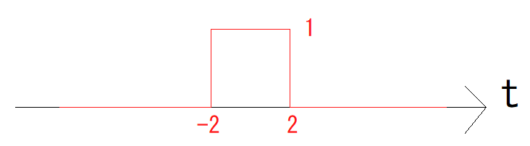 この信号の時間における値の場合わけは式(3)のようになります。
この信号の時間における値の場合わけは式(3)のようになります。
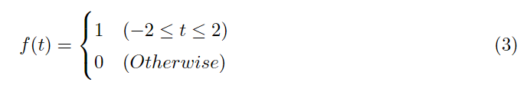 式(1)に代入をして計算をすると、
式(1)に代入をして計算をすると、
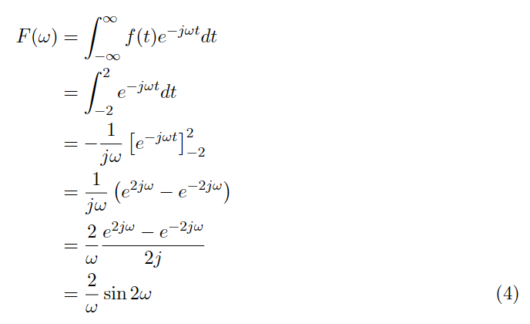 また、(4)式ではω=0のとき定義されないことがわかるため、ω=0のときの計算を行うと、
また、(4)式ではω=0のとき定義されないことがわかるため、ω=0のときの計算を行うと、
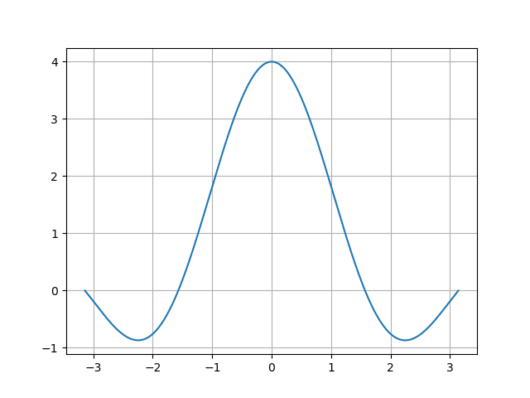
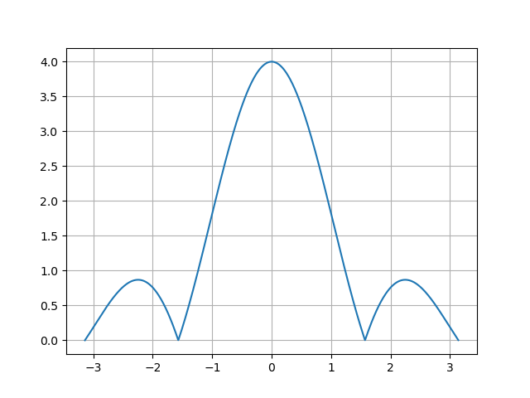
 pythonを使用してF(ω)のプロットをしてみます。式(4),(5)の式をもとに実装したプログラムは以下の通りです。
pythonを使用してF(ω)のプロットをしてみます。式(4),(5)の式をもとに実装したプログラムは以下の通りです。
import numpy as np
import matplotlib.pyplot as plt
minus_x = np.arange(-np.pi, 0.0, 0.01)
plus_x = np.arange(0.0, np.pi, 0.01)
x = []
s = []
a_s = []
for i in minus_x:
y = 2/i * np.sin(2 * i)
x.append(i)
s.append(y)
a_s.append(abs(y))
for i in plus_x:
if i == 0.0:
x.append(i)
s.append(4)
a_s.append(4)
else:
y = 2/i * np.sin(2 * i)
x.append(i)
s.append(y)
a_s.append(abs(y))
plt.plot(x, s)
plt.grid()
plt.show()
plt.plot(x, a_s)
plt.grid()
plt.show() 式(4),(5)をプロットしたものと、絶対値をとってからプロットしたものの実行結果を以下に示します。

 フーリエ逆変換に関しても、時間領域ではなく周波数領域の波形がある場合、式(1)に今回の流れで場合わけを行って計算をすることで求めることができます。興味があるかたは是非やってみてください。
フーリエ逆変換に関しても、時間領域ではなく周波数領域の波形がある場合、式(1)に今回の流れで場合わけを行って計算をすることで求めることができます。興味があるかたは是非やってみてください。
 フーリエ逆変換に関しても、時間領域ではなく周波数領域の波形がある場合、式(1)に今回の流れで場合わけを行って計算をすることで求めることができます。興味があるかたは是非やってみてください。
フーリエ逆変換に関しても、時間領域ではなく周波数領域の波形がある場合、式(1)に今回の流れで場合わけを行って計算をすることで求めることができます。興味があるかたは是非やってみてください。おまけ
反比例(ω)×sinωの掛け合わせた関数は、sinc関数という名前がついており、式(6)で表される。
 先ほどの式(4)をsinc関数を用いて表すと、
先ほどの式(4)をsinc関数を用いて表すと、
 式(7)のように変形ができます。pythonのnumpyのAPIにはsinc関数があるので、リファレンスを確認してみると、sinc関数の内部では次のような計算を行ってくれるそうです。
式(7)のように変形ができます。pythonのnumpyのAPIにはsinc関数があるので、リファレンスを確認してみると、sinc関数の内部では次のような計算を行ってくれるそうです。
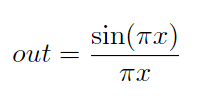 このことを踏まえて実装すると次のようになります。
このことを踏まえて実装すると次のようになります。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-np.pi, np.pi, 0.01)
s = 4 * np.sinc(2 * x/ np.pi)
a_s = abs(4 * np.sinc(2 * x/ np.pi))
plt.plot(x, s)
plt.grid()
plt.show()
plt.plot(x, a_s)
plt.grid()
plt.show()
便利ですね。
おわりに
フーリエ変換をすると、時間領域では不連続だった信号が連続のスペクトルで表すことができるようになるということがわかりました。次回は、ラプラス変換についてやっていきたいと思います。古典制御の勉強をしていくぞー!