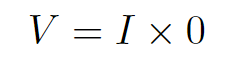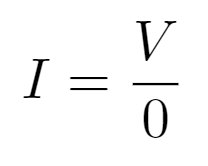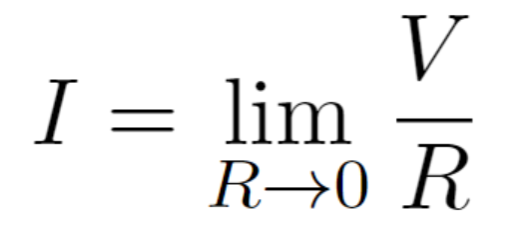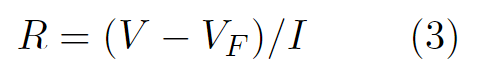ADALM2000で勉強をしてみる その2 オームの法則
今回からはADALM2000とADALP2000を使用した電子回路の勉強を始めていきたいと思います。Wikiのページは英語なので日本語に訳したりマイクロマウス競技ではこういうところで使うみたいな話を書いていこうと思います。参考ページはADALM2000 Based Lab Activity Material, Electronics I and IIで、基本的にこれに沿って勉強をしていきます!
有識者の方で、記事の中で間違いやグレーなゾーン等があった場合、指摘をしていただければと思います。どうぞよろしくお願いいたします。
今回はElectronics IのAn Ohm’s Law Experimentからスタートしていきたいと思います。General Lab materialsのところにはブレッドボードの寄生コンデンサなどの話も丁寧に書いてあったので興味がある方は是非読んでみるといいかもです。
オームの法則
中学校の理科で習う式です。電気回路等を扱う上では必須の式だと思ってます。
記号が出てきたときは英単語の意味を覚えるといいかもと思っているため書かせていただきました。電流のIntensityがいつも出てこなくて困ってます。Currentは出てくることが多いのですが・・・。電流のIってなんの略といわれてすぐに答えられる人はすごいなぁと思います。
LEDを繋いだ回路について
今回の勉強はLED(発光ダイオード)に一定の電流を流す方法について勉強をしていきたいと思います。
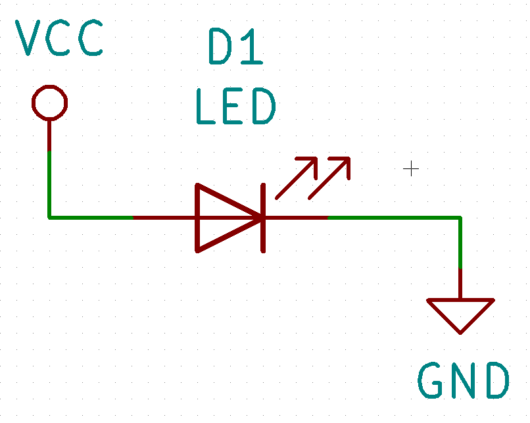
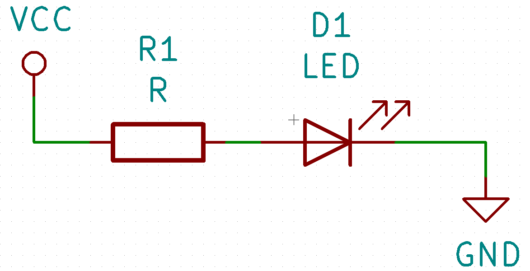
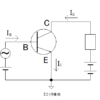
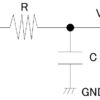
下図の回路図をご覧ください。
この回路図を見てだめ!と思った方への問いになります。「なぜこの回路がだめなのか」ということです。
しっかりと考えていきましょう。まずは、LED並びにダイオードの抵抗値を考えると、順方向電圧を越えるまでは電流が流れない絶縁体に近い特性をもっていますが順方向電圧1を超えると電流がとても流れるようになります。そのため、ダイオードの抵抗値はとても小さくなる、すなわち0に近似することが可能になります。
そのとき、(1)式に代入をすると
ここで、順方向電圧よりも大きいときに電流が流れるようになるため、この=は成立しません。電流Iについて式変形をすると、
割り算において0で割ると言ことは定義されていないためおかしなことになってしまいました。先程のダイオードの抵抗はとても小さくなるため0に近似をするということにしましたが、0に近い値であるとすると電流が無限大に流れると考えることができます。極限の考え方ですね。
ただ、現実では無限大の電流はあり得ないです。LEDに電圧を供給する電源が流せる最大電流が流れることになります。LEDに最大電流が流れ込んでしまうとLEDが焼損してしまいます。この、電流が無限大という状況を作らないためにしたものがいつも使っている下図の回路になります。
次に、LEDに流れる電流を求めたいと思います。LEDと抵抗でどのように分圧するのかがわからないと仮定して実際にADALM2000で測定をしてみたいと思います。
ところが、今回使用するLEDの定格は20mAであるため20mA以上は流すことをしたくありません。そのため、An Ohm’s Law Experimentと同様の設定で実験を行っていきたいと思います。回路全体に流す電流を18mAに設定をして電圧を5Vとして(1)式に代入すると抵抗が約277Ωと求まりますが、277Ωは一般には存在しないことと、ADALP2000のキットには一番小さい抵抗が470Ωであることから470Ωを設定しています。
実験をしてみる
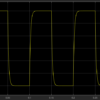
Wikiのページと同じように実験をしたところ大体同じ結果になりました。実験風景はブレッドボードに抵抗とLEDを付けただけなので省略させていただきます。
LEDには、データシートの順電圧がだいたいかかっていることがわかりました。同様に抵抗の電圧は以下のようにかかっていることがわかりました。
LEDの電流制限抵抗をデータシートから簡易的に決める方法
(2)式より、使用するLEDのDC Forward VoltageがわかればLEDにかかる電圧が大体わかります。LEDにかかる電圧がわかれば抵抗にかかる電圧が求められるので、直列回路の性質より直列回路に流れる電流は一定になればよいため、抵抗に流れる電流がLEDに流れる電流になります。
したがって、今回の実験で使用した回路の電流を求める場合は(3)式で求めることが可能であるということがわかりました。
マイクロマウス競技のUI用のLEDにつける抵抗値はこのようにして計算することが可能です。
さいごに
これを機に基礎から勉強をし直すぞということで基礎から勉強を始めました。ADALM2000とADALP2000のキットを使用して勉強を一通りすれば電子回路の基礎をしっかりとしたものに変えていけそう(?)です。
この調子で頑張っていく所存です。