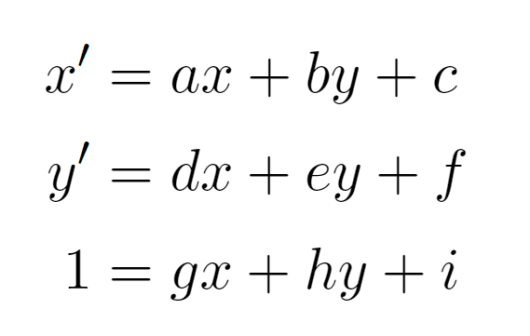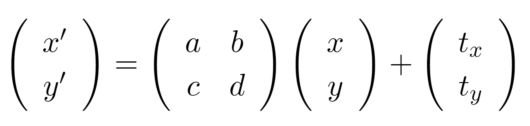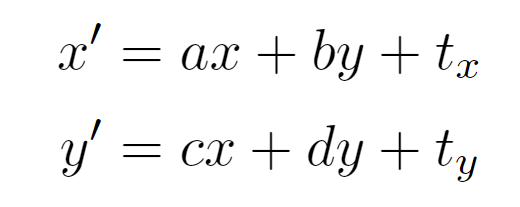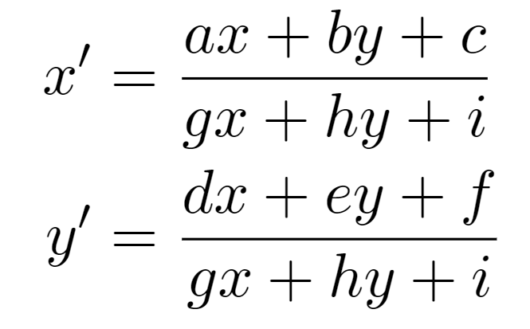画像の幾何学的変換をやってみる その3 同次座標を用いたアフィン変換の実装
こんにちは。そらです。
画像の幾何学的変換をやってみる その2で一般的な線形変換の行列の逆行列を求めてアフィン変換の実装をしてみるということをしてみました。その1で紹介した同次座標を用いた手法での実装については書いていないことに気づいたため実装をしていきたいと思います。
同次座標を用いたアフィン変換の実装
実装するために式変形を行う
同時座標で使用する変形行列は3行3列のものになり、一般的な線形変換を表現することができます。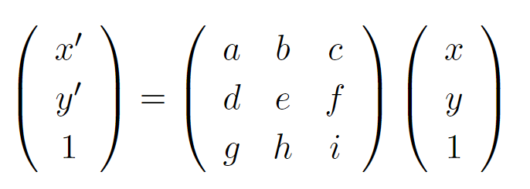 一般的な線形変換と比べるとパラメータが増えていることがわかります。行列の掛け算をしてみると、次のようになります。
一般的な線形変換と比べるとパラメータが増えていることがわかります。行列の掛け算をしてみると、次のようになります。
その2の一般的な線形変換のときの式と比較をしてみます。
先程の同時座標から求めた式と比較をしてみると、a,b,d,eは線形変換の2行2列のパラメータであり、c,fが平行移動のパラメータであることがわかります。
同時座標の中で不明なパラメータは3行目の式にあるものだけになりました。この式が表しているものについて検討をしていきます。行列式を見ると、左辺が1という定数であるため式の全体で整合性を合わせる必要があります。したがって、アフィン変換を実装するときにはx’,y’の式はそれぞれ、
で計算をすることになります。ここで、一般的な線形変換の式と比較をすると、分母のパラメータはg =0, h = 0, i = 1である必要が考えられます。
実装をしてみる
式の変形ができたので、実装をしていきたいと思います。アフィン変換をするために必要なパラメータはa,b,c,d,e,fの6つであることがわかりました。また、サイズ変更後の座標系はx’,y’の変換式で変換前の画像のサイズとa,b,c,dの絶対値を取ったもので計算をすれば求まることが考えられます。
#define PI 3.14159265359
cv::Mat execute_affin_conversion_sample(cv::Mat img)
{
cv::Mat conversion_matrix = cv::Mat::zeros(cv::Size(3, 3), CV_32F);
float rad = 10.0f * PI / 180.0f;
conversion_matrix.at(0, 0) = 1;
conversion_matrix.at(0, 1) = 0;
conversion_matrix.at(0, 2) = 0;
conversion_matrix.at(1, 0) = 0;
conversion_matrix.at(1, 1) = 1;
conversion_matrix.at(1, 2) = 0;
conversion_matrix.at(2, 0) = 0;
conversion_matrix.at(2, 1) = 0;
conversion_matrix.at(2, 2) = 1;
cv::Mat out = affin_conversion(img, conversion_matrix);
return out;
}
cv::Mat affin_conversion(cv::Mat img, cv::Mat conversion_matrix)
{
float a = conversion_matrix.at(0, 0);
float b = conversion_matrix.at(0, 1);
float c = conversion_matrix.at(0, 2);
float d = conversion_matrix.at(1, 0);
float e = conversion_matrix.at(1, 1);
float f = conversion_matrix.at(1, 2);
int resize_width = 0;
int resize_height = 0;
resize_width = (abs(a) * img.cols + abs(b) * img.rows + c);
resize_height = (abs(d) * img.cols + abs(e) * img.rows + f);
std::cout << "width = " << resize_width << "height = " << resize_height << std::endl;
int offset_x = (resize_width - img.cols) / 2;
int offset_y = (resize_height - img.rows) / 2;
cv::Mat out = cv::Mat::zeros(cv::Size(resize_width, resize_height), CV_8UC3);
for (int y = 0; y < img.rows; y++) {
for (int x = 0; x < img.cols; x++) {
int nowx = x - img.cols / 2;
int nowy = y - img.rows / 2;
float rx = (a * nowx + b * nowy + c) + img.cols / 2 + offset_x;
float ry = (d * nowx + e * nowy + f) + img.rows / 2 + offset_y;
int dx = rx;
int dy = ry;
if (dx < 0 || dx > resize_width || dy < 0 || dy > resize_height) continue;
for (int i = 0; i < img.channels(); i++) { if (dx > 1 && dy > 1) {
out.at(dy - 1, dx - 1)[i] = img.at(y, x)[i];
out.at(dy - 1, dx)[i] = img.at(y, x)[i];
out.at(dy, dx - 1)[i] = img.at(y, x)[i];
}
out.at(dy, dx)[i] = img.at(y, x)[i];
if (dx < resize_width - 1 && dy < resize_height - 1) {
out.at(dy + 1, dx)[i] = img.at(y, x)[i];
out.at(dy, dx + 1)[i] = img.at(y, x)[i];
out.at(dy + 1, dx + 1)[i] = img.at(y, x)[i];
}
}
}
}
return out;
}さいごに
アフィン変換を同次座標の考え方を用いて実装をしてみました。一般系では逆行列について考える必要がありましたが同次座標を用いることで逆行列を考える必要がなくなり、直接的に求めることができるようになっていることがわかります。
逆行列を考えることなく実装ができたため一般系よりも楽に実装ができました。
ここからは私事になりますが、画像処理が必要になったはものの基礎があやふやだと感じてきたため、画像処理の勉強をしながら実装をするということをしています。大津の2値化も名前だけでどのようになっているのかどうかをわからず使用していましたが、先日実装をすることでなるほどとなったことが記憶に新しいです。opeccvなどのライブラリは便利ですが1度は自力で計算式を分解して実装をするということをした方がいいと思いました。
また、忘備録としてこのブログに画像処理の式変形から実装までを記事という形で書くかもしれません。
参考文献
ディジタル画像処理[改訂新版]